Generator Przebiegów Arbitralnych
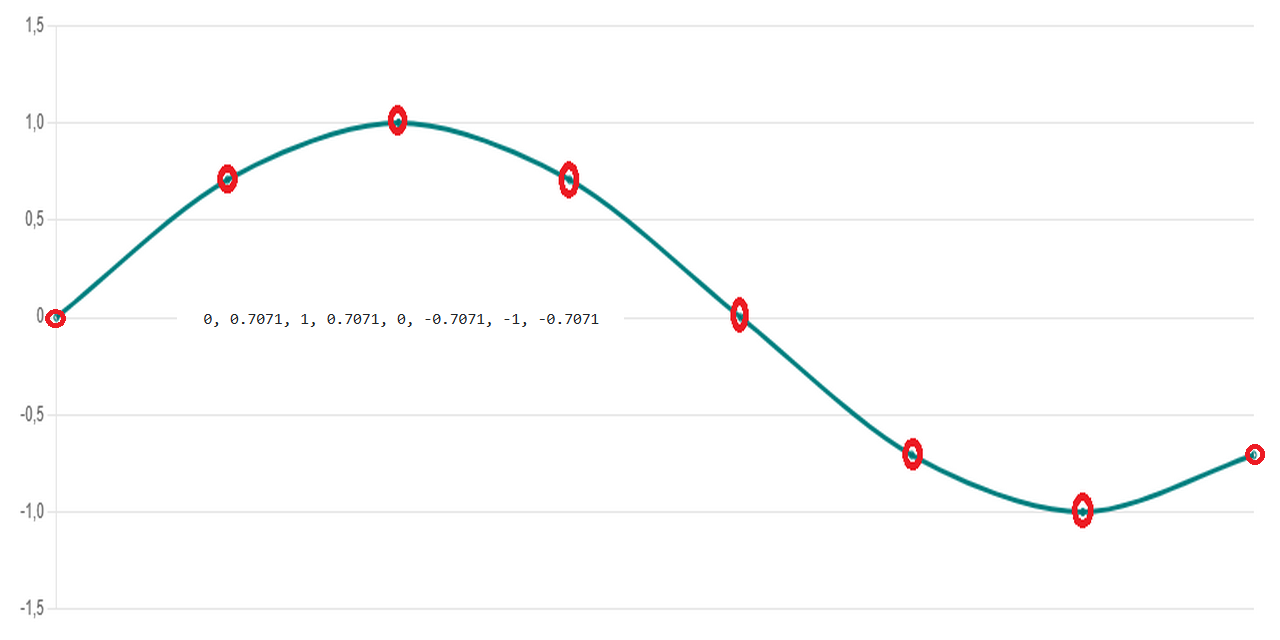
Stwórz własny dźwięk od podstaw!
Poznaj interaktywny generator przebiegów arbitralnych, który daje Ci pełną kontrolę nad kształtem fali dźwiękowej. To więcej niż zwykły generator – to narzędzie do kreatywnej eksploracji dźwięku:
Rysuj własne fale – intuicyjnie myszką, dokładnie tak, jak je sobie wyobrażasz. Zobacz, jak brzmi – od razu sprawdź wykres LUT i usłysz efekt na żywo. Gotowe kształty – sinus, trójkąt, prostokąt, piła – na start i dla porównania. Złóż falę z harmonicznych - dowolny kształt fali na bazie harmonicznych Natychmiastowe odtwarzanie – Twoje przebiegi generują realny dźwięk w czasie rzeczywistym.
Doskonałe narzędzie dla:
- muzyków i producentów – do kreowania niestandardowych brzmień,
- studentów – do nauki o dźwięku, przebiegach i sygnałach,
- pasjonatów elektroniki i DSP – do eksperymentów z generacją sygnału.
Zero instalacji. Działa od razu w przeglądarce.
Wypróbuj i stwórz dźwięk, jakiego jeszcze nie było!
Rozwinięcia przebiegów w szereg Fouriera
1. Przebieg prostokątny (fala prostokątna)
Zakładamy sygnał okresowy o okresie \( T \), wartości \( +A \) w przedziale \( (0, T/2) \), wartości \( -A \) w \( (-T/2, 0) \).
Rozwinięcie w szereg Fouriera (tylko wyrazy nieparzyste):
$$ f(t) = \frac{4A}{\pi} \sum_{n=1,3,5,\dots}^{\infty} \frac{1}{n} \sin\left( \frac{2\pi n t}{T} \right) $$
2. Przebieg piłokształtny (fala piłokształtna)
Zakładamy sygnał okresowy o okresie \( T \), narastający liniowo od \( -A \) do \( A \).
Rozwinięcie:
$$ f(t) = \frac{-2A}{\pi} \sum_{n=1}^{\infty} \frac{(-1)^n}{n} \sin\left( \frac{2\pi n t}{T} \right) $$
3. Przebieg trójkątny (fala trójkątna)
Zakładamy okres \( T \), sygnał rosnący liniowo od \( 0 \) do \( A \), a potem malejący do \( 0 \), potem do \( -A \) itd.
Rozwinięcie:
$$ f(t) = \frac{8A}{\pi^2} \sum_{n=1,3,5,\dots}^{\infty} \frac{(-1)^{(n-1)/2}}{n^2} \sin\left( \frac{2\pi n t}{T} \right) $$
4. Ząbkowany (napięcie zębate, „sawtooth” – inna wersja)
Jeśli zaczyna się od zera i rośnie liniowo do \( A \), a potem nagle spada do zera:
$$ f(t) = \frac{A}{2} - \frac{A}{\pi} \sum_{n=1}^{\infty} \frac{1}{n} \sin\left( \frac{2\pi n t}{T} \right) $$
5. Sygnał prostokątny niesymetryczny (współczynnik wypełnienia D)
Jeśli sygnał ma wartość \( A \) przez czas \( DT \), a \( 0 \) przez \( (1-D)T \):
$$ f(t) = A D + \sum_{n=1}^{\infty} \frac{2A}{n\pi} \sin(n\pi D) \cos\left( \frac{2\pi n t}{T} \right) $$
6. Sygnał impulsowy (Dirac comb – ciąg impulsów)
Sygnał złożony z delta Diraców co \( T \):
$$ \sum_{n=-\infty}^{\infty} \delta(t - nT) \quad \Rightarrow \quad \text{Fourier: } \frac{1}{T} \sum_{n=-\infty}^{\infty} e^{j 2\pi n f_0 t}, \quad f_0 = \frac{1}{T} $$
Modulacja przebiegu
Modulacja amplitudy (AM)
Formuła AM:
$$ s_{AM}(t) = [1 + m \cdot \sin(2\pi f_m t)] \cdot \sin(2\pi f_c t) $$
Gdzie:
- \( s_{AM}(t) \) – sygnał zmodulowany amplitudowo,
- \( m \) – głębokość modulacji (modulation index, \( 0 \leq m \leq 1 \)),
- \( f_m \) – częstotliwość sygnału modulującego,
- \( f_c \) – częstotliwość nośna.
Modulacja częstotliwości (FM)
Formuła FM:
$$ s_{FM}(t) = A \cdot \sin\left(2\pi f_c t + \beta \cdot \sin(2\pi f_m t)\right) $$
Gdzie:
- \( s_{FM}(t) \) sygnał zmodulowany częstotliwościowo,
- \( A \) – amplituda sygnału (stała),
- \( f_c \) – częstotliwość nośna (carrier),
- \( f_m \) – częstotliwość modulująca (modulator),
-
\( \beta \) – indeks modulacji:
$$ \beta = \frac{\Delta f}{f_m} $$
gdzie \( \Delta f \) to maksymalne odchylenie częstotliwości nośnej.
Modulacja dwuwstęgowa (DSB)
DSB (Double Sideband) to forma modulacji amplitudy, w której:
- nośna jest mnożona przez sygnał modulujący,
- brak dodatkowej nośnej (w przeciwieństwie do klasycznej AM).
Formuła DSB:
$$ s(t) = m(t) \cdot \cos(2\pi f_c t) $$
Gdzie:
- \( m(t) \) – sygnał modulujący (np. sinus, piła itp.)
- \( f_c \) – częstotliwość nośna (carrier)
Zniekształcenia harmoniczne
Co to jest THD?
THD [%] to stosunek całkowitej mocy harmonicznych (bez podstawowej) do mocy harmonicznej podstawowej, zwykle wyrażony w procentach:
$$ \text{THD} = \frac{\sqrt{V_2^2 + V_3^2 + \dots + V_n^2}}{V_1} \cdot 100\% $$
Typowe zniekształcenia sygnałów audio – tabela porównawcza
| Rodzaj zniekształcenia | Opis efektu | Charakterystyka zniekształcenia | Szacunkowy THD | Uwagi |
|---|---|---|---|---|
| Clipping symetryczny | Obcięcie sygnału po obu stronach (np. wzmacniacz tranzystorowy bez zapasu) | Twarda nieliniowość | 30–60% | Bogate w nieparzyste harmoniczne |
| Clipping asymetryczny | Obcięcie tylko jednej strony (np. taśma bez prądu podkładu) | Nieliniowość niesymetryczna | 40–80% | Silna dominacja parzystych harmonicznych |
| Tape saturation (taśma + AC bias) | Zaokrąglona nieliniowość przy większych amplitudach | Miękka saturacja (symetryczna) | 5–15% | Typowa dla analogowych rejestratorów |
| Tape without bias (DC) | Obcięcie jednej strony sinusa – silnie asymetryczne | Nasycenie jednostronne | 40–70% | Sygnał brzmi „zatkany”, słabo słyszalny |
| Magnetic core saturation (trafo) | Miękkie ograniczenie amplitudy przy wysokich poziomach | Zniekształcenia symetryczne lub asymetryczne | 10–30% | Zależne od typu rdzenia |
| Overdrive (lampa) | Zaokrąglona saturacja z dominacją niższych harmonicznych | Miękka nieliniowość, lekko asymetryczna | 5–20% | Dźwięk „ciepły”, bogaty |
| Soft limiting (kompresja) | Redukcja dynamiki przy wysokim poziomie | Łagodna nieliniowość | 5–15% | Efekt „loudness”, bez dużej utraty barwy |
| Diode clipping (np. fuzz) | Twarde obcięcie przez diody (np. 0.7V) | Symetryczne lub asymetryczne | 40–80% | Bardzo agresywny, używany w efektach gitarowych |
| Nonlinear transfer (np. tanh) | Łagodne zaokrąglenie amplitudy | Nieliniowość hiperb. | 10–30% | Używane w cyfrowych symulacjach „taśmy” |
| Zapis z przesuniętym biasem DC | Stałe przesunięcie punktu pracy na taśmie → asymetria | Zniekształcenie jednostronne | 30–60% | Daje sygnał „przesunięty” |
Jak obsługiwać aplikację?
- ustaw ilość próbek, częstotliwość i amplitudę
- wybierz sposób generowania przebiegu klikając na odpowiednią zakładkę
- uaktualnij LUT klikając przycisk Generuj LUT
- odtwórz dźwięk klikając przycisk
- przy każdej zmianie przebiegu uaktualnij LUT przyciskiem Generuj LUT
- zakończenie rysowania przebiegu uaktualni LUT automatycznie
Jak obserwować przebiegi?
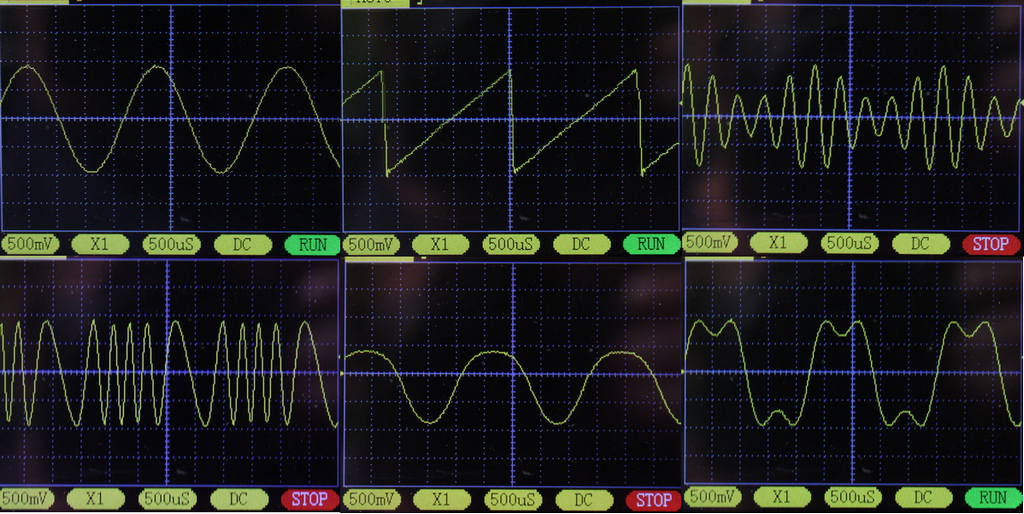
Podłącz dowolny oscyloskop do wyjścia słuchawkowego swojego smartfona i kliknij przycisk Odtwórz po wygenerowaniu LUT. Na swoim oskopie zobaczysz przebieg odpowiadający wygenerowanemu tutaj przebiegowi. Obraz poniżej przedstawia kilka wygenerowanych przebiegów: sinusoidalny, piłokształtny, modulacja AM, modulacja FM, łagodne asymetryczne obcinanie, przebieg składany z harmonicznych.
Kliknij Generuj LUT po każdej zmianie w polach powyżej.
| Nr harmonicznej | Amplituda | Akcje |
|---|
Kliknij Generuj LUT po każdej zmianie w polach powyżej.
LUT zostanie uaktualniony po zakończeniu rysowania.
Kod po stronie przeglądarki
<style>
textarea {
font-family: monospace;
}
canvas#drawCanvas {
border: 1px solid #ccc;
background: #f9f9f9;
cursor: crosshair;
}
</style>
<div id="app" class="container">
<div class="row my-3">
<div class="col-md-4 mb-3">
<label for="sampleCount" class="form-label">Próbki</label>
<input type="number" id="sampleCount" class="form-control" value="64" min="8" max="512">
</div>
<div class="col-md-4 mb-3">
<label for="frequency" class="form-label">Częstotliwość (Hz)</label>
<input type="number" id="frequency" class="form-control" value="440" min="20" max="2000">
</div>
<div class="col-md-4 mb-3">
<label for="amplitude" class="form-label">Amplituda</label>
<input type="number" id="amplitude" class="form-control" value="1" step="0.1" min="0" max="2">
</div>
</div>
<ul class="nav nav-tabs" id="modeTabs" role="tablist">
<li class="nav-item">
<button id="btnPresetTab" class="nav-link active" data-bs-toggle="tab" data-bs-target="#preset" type="button">Gotowe przebiegi</button>
</li>
<li class="nav-item">
<button class="nav-link" data-bs-toggle="tab" data-bs-target="#harmonics" type="button">Harmoniczne</button>
</li>
<li class="nav-item">
<button class="nav-link" data-bs-toggle="tab" data-bs-target="#custom" type="button">Rysuj własny</button>
</li>
</ul>
<div class="tab-content mt-3">
<div class="tab-pane fade show active" id="preset">
<div class="row mb-3">
<div class="col-lg-3 mb-3">
<label for="waveformType" class="form-label">Typ przebiegu</label>
<select class="form-select" id="waveformType">
<option value="sine">sinusoidalny</option>
<option value="triangle">trójkątny</option>
<option value="square">prostokątny</option>
<option value="sawtooth">piłokształtny</option>
<option value="clipped_sine">przycięty sinus</option>
<option value="noise">szum</option>
<option value="impulse_train">ciąg impulsów</option>
<option value="burst">impuls periodyczny</option>
<option value="am">AM (modulacja amplitudy)</option>
<option value="fm">FM (modulacja częstot.)</option>
<option value="dsb">DSB (modulacja dwuwstęg.)</option>
<option value="pwm">PWM (wypełnienie)</option>
</select>
</div>
<div class="col-lg-3 mb-3">
<label for="modType" class="form-label">Sygnał modulujący</label>
<select id="modType" class="form-select" disabled>
<option value="sin">sinus</option>
<option value="triangle">trójkąt</option>
<option value="square">prostokąt</option>
<option value="sawtooth">piła</option>
</select>
</div>
<div class="col-lg-3 mb-3">
<label for="modIndex" class="form-label">Indeks modulacji / Wsp. wyp.</label>
<input type="number" id="modIndex" class="form-control" value="0.5" step="0.1" min="0" max="1" disabled>
</div>
<div class="col-lg-3 mb-3">
<label for="distortion" class="form-label">Zniekształcenie</label>
<select id="distortion" class="form-select">
<option value="none">Brak</option>
<option value="clip">Obcinanie</option>
<option value="halfwave">Półfalowe</option>
<option value="fullwave">Pełnofalowe</option>
<option value="no_bias_tape">Taśma bez podkładu</option>
<option value="dc_bias_tape">Taśma prąd podkładu DC</option>
<option value="ac_bias_tape">Taśma prąd podkładu AC</option>
<option value="trafo_saturation">Nasycenie transformatora</option>
</select>
</div>
<div class="col-md-3 mb-3">
<button class="btn btn-primary" onclick="generateLUT()"><i class="bi bi-cpu"></i> Generuj LUT</button>
</div>
<div class="col-md-12 mb-3">
<div class="alert alert-warning">
<p class="mb-0">Kliknij Generuj LUT po każdej zmianie w polach powyżej.</p>
</div>
</div>
</div>
</div>
<div class="tab-pane fade" id="harmonics" role="tabpanel">
<div class="mt-3">
<table class="table table-sm table-bordered align-middle" id="harmonicsTable">
<thead>
<tr>
<th>Nr harmonicznej</th>
<th>Amplituda</th>
<th>Akcje</th>
</tr>
</thead>
<tbody>
<!-- Wiersze będą dodawane dynamicznie -->
</tbody>
</table>
<button class="btn btn-success btn-sm mb-3" onclick="addHarmonicRow()"><i class="bi bi-plus-circle"></i> Dodaj harmoniczną</button>
<button class="btn btn-primary btn-sm mb-3" onclick="generateFromHarmonics()"><i class="bi bi-cpu"></i> Generuj LUT</button>
<div class="alert alert-warning">
<p class="mb-0">Kliknij Generuj LUT po każdej zmianie w polach powyżej.</p>
</div>
</div>
</div>
<div class="tab-pane fade" id="custom">
<div class="mb-3">
<div class="mb-2">Narysuj jeden okres przebiegu (kliknij i przeciągnij):</div>
<canvas id="drawCanvas" width="310" height="150"></canvas>
<div class="form-text">Lewy brzeg = początek okresu, prawy = koniec. Góra = 1, dół = -1.</div>
</div>
<div class="mb-3">
<div class="alert alert-info">
<p class="mb-0">LUT zostanie uaktualniony po zakończeniu rysowania.</p>
</div>
</div>
</div>
</div>
<label for="lutOutput" class="form-label">LUT (Look-Up Table)</label>
<textarea id="lutOutput" class="form-control mb-3" rows="3" readonly></textarea>
<canvas id="lutChart" height="100"></canvas>
<canvas id="fftChart" height="100"></canvas>
<div class="mb-3" id="dcInfo">
</div>
<div class="mb-3" id="thdInfo">
</div>
<div class="mb-3">
<button class="btn btn-success me-2 mb-2" onclick="playLUT()"><i class="bi bi-play-fill"></i> Odtwórz</button>
<button class="btn btn-danger me-2 mb-2" onclick="stopSound()"><i class="bi bi-stop-fill"></i> Zatrzymaj</button>
<button class="btn btn-warning me-2 mb-2" onclick="exportWAV()"><i class="bi bi-file-earmark-music"></i> Zapisz do WAV</button>
<button class="btn btn-info me-2 mb-2" onclick="exportLUT()"><i class="bi bi-box-arrow-up"></i> Eksportuj LUT</button>
<input type="file" id="importLUTInput" accept=".json" hidden onchange="importLUT(event)" aria-label="Wybierz plik JSON">
<button class="btn btn-info me-2 mb-2" onclick="document.getElementById('importLUTInput').click()"><i class="bi bi-box-arrow-in-down"></i> Importuj LUT</button>
</div>
</div>
<script src="https://cdn.jsdelivr.net/npm/chart.js"></script>
<script>
//variables
let audioCtx;
let sourceNode;
let chart;
let currentSamples = [];
const canvas = document.getElementById('drawCanvas');
const ctx = canvas.getContext('2d');
let drawing = false;
let drawnPoints = [];
let lastX = null,
lastY = null;
var chartFFT;
function dft(signal) {
const X = [];
const N = signal.length;
for (let k = 0; k < N; k++) {
let re = 0,
im = 0;
for (let n = 0; n < N; n++) {
const angle = -2 * Math.PI * k * n / N;
re += signal[n] * Math.cos(angle);
im += signal[n] * Math.sin(angle);
}
X.push({
re,
im
});
}
return X;
}
function calculateTHD(magnitudes) {
const fundamental = magnitudes[1]; // Pomijamy DC (magnitudes[0])
const harmonics = magnitudes.slice(2); // od 2. harmonicznej wzwyż
const harmonicPower = harmonics.reduce((sum, val) => sum + val ** 2, 0);
const thd = Math.sqrt(harmonicPower) / fundamental;
return thd * 100;
}
function generateLUT() {
const type = document.getElementById('waveformType').value;
const count = parseInt(document.getElementById('sampleCount').value);
const modIndex = parseFloat(document.getElementById('modIndex').value);
const distortion = document.getElementById('distortion')?.value || 'none';
const samples = [];
const fc = 5; // nośna
const fm = 1; // modulująca
for (let i = 0; i < count; i++) {
const t = i / count;
let val = 0;
// wybór typu sygnału modulującego
const mType = document.getElementById('modType').value;
switch (mType) {
case 'sin':
modulator = Math.sin(2 * Math.PI * fm * t);
break;
case 'triangle':
modulator = 1 - 4 * Math.abs(Math.round(t - 0.25) - (t - 0.25));
break;
case 'square':
modulator = (t % 1) < 0.5 ? 1 : -1;
break;
case 'sawtooth':
modulator = 1 - 2 * (t % 1);
break;
}
switch (type) {
case 'sine':
val = Math.sin(2 * Math.PI * t);
// Zastosuj zniekształcenie jeśli wybrane
switch (distortion) {
case 'clip':
val = Math.max(-0.5, Math.min(0.5, val)); // twarde obcinanie
break;
case 'halfwave':
val = Math.max(0, val); // tylko dodatnia część
break;
case 'fullwave':
val = Math.abs(val); // całość dodatnia
break;
case 'no_bias_tape':
// Efekt jak przy braku prądu podkładu: asymetryczne ograniczenie
val = val >= 0 ? 0.9 * val : 0.3 * Math.tanh(3 * val);
break;
case 'dc_bias_tape':
const bias = 0.5; // wartość stała przesuwająca sygnał
val = Math.tanh(val + bias) - Math.tanh(bias);
break;
case 'ac_bias_tape':
val = Math.tanh(1.0 * val); // łagodna symetryczna saturacja
break;
case 'trafo_saturation':
val = Math.tanh(1.5 * val); // nieliniowość rdzenia
break;
// brak domyślnej – pozostaw val bez zmian
}
break;
case 'triangle':
val = 1 - 4 * Math.abs(Math.round(t - 0.25) - (t - 0.25));
break;
case 'square':
val = t < 0.5 ? 1 : -1;
break;
case 'sawtooth':
val = 2 * t - 1;
break;
case 'clipped_sine':
val = Math.sin(2 * Math.PI * t);
val = Math.max(-0.5, Math.min(0.5, val)); // Przycięcie
break;
case 'noise':
val = 2 * Math.random() - 1;
break;
case 'impulse_train':
// Co N/8 próbek impuls (zwraca 1), reszta 0
val = (i % Math.floor(count / 8)) === 0 ? 1 : 0;
break;
case 'burst':
// Sinus aktywny tylko przez pierwsze 1/8 okresu
val = t < 0.125 ? Math.sin(2 * Math.PI * 8 * t) : 0;
break;
case 'am':
const A = 0.7;
const m = modIndex; // głębokość AM: 0.0–1.0
val = A * (1 + m * modulator) * Math.sin(2 * Math.PI * fc * t);
break;
case 'fm':
val = Math.sin(2 * Math.PI * fc * t + modIndex * modulator * 2 * Math.PI);
break;
case 'dsb':
val = modIndex * modulator * Math.cos(2 * Math.PI * fc * t);
break;
case 'pwm':
const duty = modIndex; // duty cycle ∈ [0,1]
val = (t % 1) < duty ? 1 : -1;
break;
default:
val = 0;
}
samples.push(parseFloat(val.toFixed(4)));
}
currentSamples = samples;
updateDisplay(samples);
updateFFT(samples);
}
function playLUT() {
stopSound();
const frequency = parseFloat(document.getElementById('frequency').value);
const amplitude = parseFloat(document.getElementById('amplitude').value);
const sampleRate = 44100;
const periodLength = Math.floor(sampleRate / frequency);
const lut = currentSamples;
audioCtx = new(window.AudioContext || window.webkitAudioContext)();
const buffer = audioCtx.createBuffer(1, periodLength, sampleRate);
const data = buffer.getChannelData(0);
for (let i = 0; i < periodLength; i++) {
const phase = (i * lut.length / periodLength) % lut.length;
const index = Math.floor(phase);
const frac = phase - index;
const nextIndex = (index + 1) % lut.length;
data[i] = amplitude * (lut[index] * (1 - frac) + lut[nextIndex] * frac);
}
sourceNode = audioCtx.createBufferSource();
sourceNode.buffer = buffer;
sourceNode.loop = true;
sourceNode.connect(audioCtx.destination);
sourceNode.start();
}
function stopSound() {
if (sourceNode) {
sourceNode.stop();
sourceNode.disconnect();
sourceNode = null;
}
if (audioCtx) {
audioCtx.close();
audioCtx = null;
}
}
function updateFFT(samples) {
const spectrum = dft(samples);
const N = samples.length;
const Fs = N; // Zakładamy 1 cykl na N próbek ⇒ Fs = N (1 okres = 1 sekunda)
// Częstotliwości (do N/2 - jednostronne widmo)
const freqs = Array.from({
length: N / 2
}, (_, i) => i * Fs / N);
// Amplitudy – skalowanie dla jednostronnego widma
const magnitudes = spectrum.slice(0, N / 2).map((c, i) => {
let mag = Math.sqrt(c.re ** 2 + c.im ** 2) / N;
if (i !== 0) mag *= 2; // tylko dla składowych > 0 Hz
return mag;
});
const thd = calculateTHD(magnitudes);
drawFFT(freqs, magnitudes);
doAlerts(magnitudes, thd);
}
function drawFFT(freqs, magnitudes) {
const ctxFFT = document.getElementById('fftChart').getContext('2d');
if (chartFFT) {
chartFFT.data.labels = freqs;
chartFFT.data.datasets[0].data = magnitudes;
chartFFT.update();
return;
}
chartFFT = new Chart(ctxFFT, {
type: 'bar',
data: {
labels: freqs,
datasets: [{
label: 'FFT (Amplituda)',
data: magnitudes,
backgroundColor: 'rgba(255, 99, 132, 0.5)',
borderColor: 'rgb(255, 99, 132)',
borderWidth: 1
}]
},
options: {
responsive: true,
scales: {
x: {
title: {
display: true,
text: 'Harmoniczna'
}
},
y: {
title: {
display: true,
text: 'Amplituda'
}
}
}
}
});
}
function showAlertTHD(message, type = "info") {
const alert = `
<div class="alert alert-${type}" role="alert">
<p class="mb-0">${message}</p>
</div>`;
document.getElementById("thdInfo").innerHTML = alert;
}
function doAlerts(magnitudes, thd) {
document.getElementById('dcInfo').innerHTML = '';
if (magnitudes[0] > 0.01) {
document.getElementById('dcInfo').innerHTML =
'<div class="alert alert-info"><p class="mb-0"><i class="bi bi-info-square"></i> <strong>Informacja:</strong> Wykryto składową stałą DC w widmie – odpowiada zerowej harmonicznej (0 Hz). Jest to normalne przy przebiegach niesymetrycznych (np. wyprostowanych).</p></div>';
}
const thdInfo = document.getElementById('thdInfo');
const presetTabActive = document.getElementById('btnPresetTab').classList.contains('active');
const wave = document.getElementById('waveformType').value;
if (presetTabActive && ((wave === 'am') || (wave === 'fm') || (wave === 'dsb')))
{
thdInfo.innerHTML = '';
return;
}
let level, message, alertClass;
if (thd < 1) {
level = "success";
message = `THD: ${thd.toFixed(2)}% – Sygnał o bardzo niskim poziomie zniekształceń.`;
} else if (thd < 5) {
level = "info";
message = `THD: ${thd.toFixed(2)}% – Niski poziom zniekształceń, typowy dla systemów audio.`;
} else if (thd < 15) {
level = "warning";
message = `THD: ${thd.toFixed(2)}% – Umiarkowane zniekształcenia. Możliwe efekty nieliniowości.`;
} else if (thd < 30) {
level = "danger";
message = `THD: ${thd.toFixed(2)}% – Wysoki poziom zniekształceń!`;
} else if (thd < 100) {
level = "danger";
message = `<i class="bi bi-exclamation-triangle"></i> THD: ${thd.toFixed(2)}% – Bardzo silne zniekształcenia! Sygnał może być nasycony lub obcięty.`;
} else {
level = "danger";
message = `<i class="bi bi-exclamation-circle"></i> THD przekracza 100%! Oznacza to, że sygnał zawiera więcej energii w harmonicznych niż w tonie podstawowym. Sygnał jest silnie zniekształcony lub niemal całkowicie pozbawiony podstawowej częstotliwości.`;
}
showAlertTHD(message, level);
}
function updateDisplay(samples) {
document.getElementById('lutOutput').value = samples.join(', ');
drawChart(samples);
}
function drawChart(data) {
const labels = [...Array(data.length).keys()];
if (chart) chart.destroy();
chart = new Chart(document.getElementById('lutChart'), {
type: 'line',
data: {
labels: labels,
datasets: [{
label: 'LUT',
data: data,
borderColor: 'teal',
tension: 0.3,
pointRadius: 2
}]
},
options: {
responsive: true,
animation: false,
scales: {
y: {
min: -1.5,
max: 1.5
},
x: {
display: false
}
},
plugins: {
legend: {
display: false
}
}
}
});
}
function drawFromLUT(lut) {
ctx.clearRect(0, 0, canvas.width, canvas.height);
ctx.beginPath();
ctx.lineWidth = 2;
ctx.strokeStyle = '#000';
for (let i = 0; i < lut.length; i++) {
const x = i / lut.length * canvas.width;
const y = (1 - (lut[i] + 1) / 2) * canvas.height;
if (i === 0) {
ctx.moveTo(x, y);
} else {
ctx.lineTo(x, y);
}
}
ctx.stroke();
}
function drawPoint(x, y) {
drawnPoints[x] = y;
ctx.fillStyle = 'black';
ctx.fillRect(x, y, 1, 1);
}
function generateLUTFromDrawing() {
const lutSize = parseInt(document.getElementById('sampleCount').value);
const samples = [];
for (let i = 0; i < lutSize; i++) {
const x = Math.floor(i * canvas.width / lutSize);
let y = drawnPoints[x];
if (y === undefined) {
// Brak punktu: domyślnie 0
y = canvas.height / 2;
}
const val = 1 - (y / canvas.height) * 2; // Zamiana Y na [-1, 1]
samples.push(parseFloat(val.toFixed(4)));
}
currentSamples = samples;
updateDisplay(samples);
updateFFT(samples);
}
function addHarmonicRow(n = '', a = '') {
const row = document.createElement('tr');
row.innerHTML = `
<td><input type="number" class="form-control form-control-sm" value="${n}" min="1" aria-label="Harmoniczna nr. ${n}"></td>
<td><input type="number" class="form-control form-control-sm" value="${a}" step="0.01" aria-label="Amplituda wartość ${a}"></td>
<td><button class="btn btn-danger btn-sm" onclick="this.closest('tr').remove()" aria-label="Usuń harmoniczną"><span class="bi bi-x"></span></button></td>
`;
document.querySelector('#harmonicsTable tbody').appendChild(row);
}
function generateFromHarmonics() {
const rows = document.querySelectorAll('#harmonicsTable tbody tr');
const sampleCount = parseInt(document.getElementById('sampleCount').value);
const lut = new Array(sampleCount).fill(0);
for (let row of rows) {
const n = parseInt(row.cells[0].querySelector('input').value);
const a = parseFloat(row.cells[1].querySelector('input').value);
if (isNaN(n) || isNaN(a)) continue;
for (let i = 0; i < sampleCount; i++) {
const t = i / sampleCount;
lut[i] += a * Math.sin(2 * Math.PI * n * t);
}
}
// Normalizacja (opcjonalnie)
const max = Math.max(...lut.map(Math.abs));
if (max > 0) {
for (let i = 0; i < lut.length; i++) {
lut[i] /= max;
}
}
currentSamples = lut;
updateDisplay(lut);
drawFromLUT(lut);
updateFFT(lut);
}
function exportWAV() {
const frequency = parseFloat(document.getElementById('frequency').value);
const amplitude = parseFloat(document.getElementById('amplitude').value);
const duration = 2; // sekundy
const sampleRate = 44100;
const totalSamples = duration * sampleRate;
const lut = currentSamples;
const buffer = new Float32Array(totalSamples);
for (let i = 0; i < totalSamples; i++) {
const phase = (i * lut.length * frequency / sampleRate) % lut.length;
const index = Math.floor(phase);
const frac = phase - index;
const nextIndex = (index + 1) % lut.length;
buffer[i] = amplitude * (lut[index] * (1 - frac) + lut[nextIndex] * frac);
}
// Konwersja do WAV
const wavData = encodeWAV(buffer, sampleRate);
const blob = new Blob([wavData], {
type: 'audio/wav'
});
const url = URL.createObjectURL(blob);
const a = document.createElement('a');
a.href = url;
a.download = 'waveform.wav';
a.click();
URL.revokeObjectURL(url);
}
// Pomocnicza funkcja WAV (mono 16-bit PCM)
function encodeWAV(samples, sampleRate) {
const buffer = new ArrayBuffer(44 + samples.length * 2);
const view = new DataView(buffer);
function writeStr(offset, str) {
for (let i = 0; i < str.length; i++) {
view.setUint8(offset + i, str.charCodeAt(i));
}
}
writeStr(0, 'RIFF');
view.setUint32(4, 36 + samples.length * 2, true);
writeStr(8, 'WAVE');
writeStr(12, 'fmt ');
view.setUint32(16, 16, true);
view.setUint16(20, 1, true);
view.setUint16(22, 1, true);
view.setUint32(24, sampleRate, true);
view.setUint32(28, sampleRate * 2, true);
view.setUint16(32, 2, true);
view.setUint16(34, 16, true);
writeStr(36, 'data');
view.setUint32(40, samples.length * 2, true);
for (let i = 0; i < samples.length; i++) {
const s = Math.max(-1, Math.min(1, samples[i]));
view.setInt16(44 + i * 2, s * 0x7FFF, true);
}
return view;
}
function exportLUT() {
const lut = currentSamples;
const blob = new Blob([JSON.stringify(lut, null, 2)], {
type: 'application/json'
});
const url = URL.createObjectURL(blob);
const a = document.createElement('a');
a.href = url;
a.download = 'lut.json';
a.click();
URL.revokeObjectURL(url);
}
function importLUT(event) {
const file = event.target.files[0];
if (!file) return;
const reader = new FileReader();
reader.onload = function(e) {
try {
const json = JSON.parse(e.target.result);
if (!Array.isArray(json)) throw new Error("Niepoprawny format LUT");
currentSamples = json;
document.getElementById('sampleCount').value = currentSamples.length;
updateDisplay(currentSamples);
drawFromLUT(currentSamples);
} catch (err) {
alert("Błąd podczas importu LUT: " + err.message);
}
};
reader.readAsText(file);;
}
// Obsługa rysowania
canvas.addEventListener('mousedown', e => {
drawing = true;
ctx.clearRect(0, 0, canvas.width, canvas.height); // czyszczenie
drawnPoints = [];
lastX = e.offsetX;
lastY = e.offsetY;
});
canvas.addEventListener('mousemove', e => {
if (!drawing) return;
const x = e.offsetX;
const y = e.offsetY;
ctx.strokeStyle = '#000';
ctx.lineWidth = 2; // grubsza linia
ctx.beginPath();
ctx.moveTo(lastX, lastY);
ctx.lineTo(x, y);
ctx.stroke();
for (let i = lastX; i <= x; i++) {
drawnPoints[i] = y; // zapamiętaj punkt
}
lastX = x;
lastY = y;
});
canvas.addEventListener('mouseup', () => {
drawing = false;
generateLUTFromDrawing();
});
canvas.addEventListener('touchstart', (e) => {
e.preventDefault();
const touch = e.touches[0];
const mouseEvent = new MouseEvent('mousedown', {
clientX: touch.clientX,
clientY: touch.clientY
});
canvas.dispatchEvent(mouseEvent);
}, {
passive: false
});
canvas.addEventListener('touchmove', (e) => {
e.preventDefault();
const touch = e.touches[0];
const mouseEvent = new MouseEvent('mousemove', {
clientX: touch.clientX,
clientY: touch.clientY
});
canvas.dispatchEvent(mouseEvent);
}, {
passive: false
});
canvas.addEventListener('touchend', (e) => {
e.preventDefault();
const mouseEvent = new MouseEvent('mouseup', {});
canvas.dispatchEvent(mouseEvent);
}, {
passive: false
});
// Inicjalizacja domyślnego przebiegu
generateLUT();
const waveformType = document.getElementById('waveformType');
waveformType.addEventListener('change', function(e) {
e.preventDefault();
const modType = document.getElementById('modType');
const modIndex = document.getElementById('modIndex');
const distortion = document.getElementById('distortion');
let value = waveformType.value;
switch (value) {
case 'sine':
modType.disabled = true;
modIndex.disabled = true;
distortion.disabled = false;
break;
case 'am':
modType.disabled = false;
modIndex.disabled = false;
distortion.disabled = true;
break;
case 'fm':
modType.disabled = false;
modIndex.disabled = false;
distortion.disabled = true;
break;
case 'dsb':
modType.disabled = false;
modIndex.disabled = false;
distortion.disabled = true;
break;
case 'pwm':
modType.disabled = true;
modIndex.disabled = false;
distortion.disabled = true;
break;
default:
modType.disabled = true;
modIndex.disabled = true;
distortion.disabled = true;
break;
}
});
</script>
Kod po stronie serwera
Brak kodu serwera
Ta aplikacja działa wyłącznie w przeglądarce i nie korzysta z kodu po stronie serwera.
Licencja
## BSD-3-Clause License Agreement
BSD-3-Clause
Сopyright (c) 2026 Dariusz Rorat
All rights reserved.
Redistribution and use in source and binary forms, with or without
modification, are permitted provided that the following conditions are met:
1. Redistributions of source code must retain the above copyright notice,
this list of conditions and the following disclaimer.
2. Redistributions in binary form must reproduce the above copyright notice,
this list of conditions and the following disclaimer in the documentation
and/or other materials provided with the distribution.
3. Neither the name of the copyright holder nor the names of its
contributors may be used to endorse or promote products derived from
this software without specific prior written permission.
THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS "AS IS"
AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE
IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE ARE
DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT HOLDER OR CONTRIBUTORS BE LIABLE
FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL
DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR
SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER
CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY,
OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE
OF THIS SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE.